数学は例年通りの問題数でした。
そもそもの問題の難易度は、記述問題であったとしても昨年より若干取りやすいと思います。
それがマーク式に変更となったため、かなり高得点が取りやすくなっています。
実際、岡崎北高校以上の高校を目指している人は、このテストで20点以上(22点か21点か20点)取ることが普通では?と思う水準だと考えています。
今までであれば数学でそんな水準はほとんどないのでは?
でも、実際のところ最低でも21点は取らなければいけない難易度です。
(塾生の皆、取れてました!?)
大問1は省略です。
大問2…なにこれ?という難易度です。これで計7点…信じられません。
(1)は秒殺です。塾の最後の宿題に箱ひげ図出して良かったです。
(2)はまさかの証明復活で、空欄の前後だけ見れば取れる一番楽なパターンです。これも秒殺です。
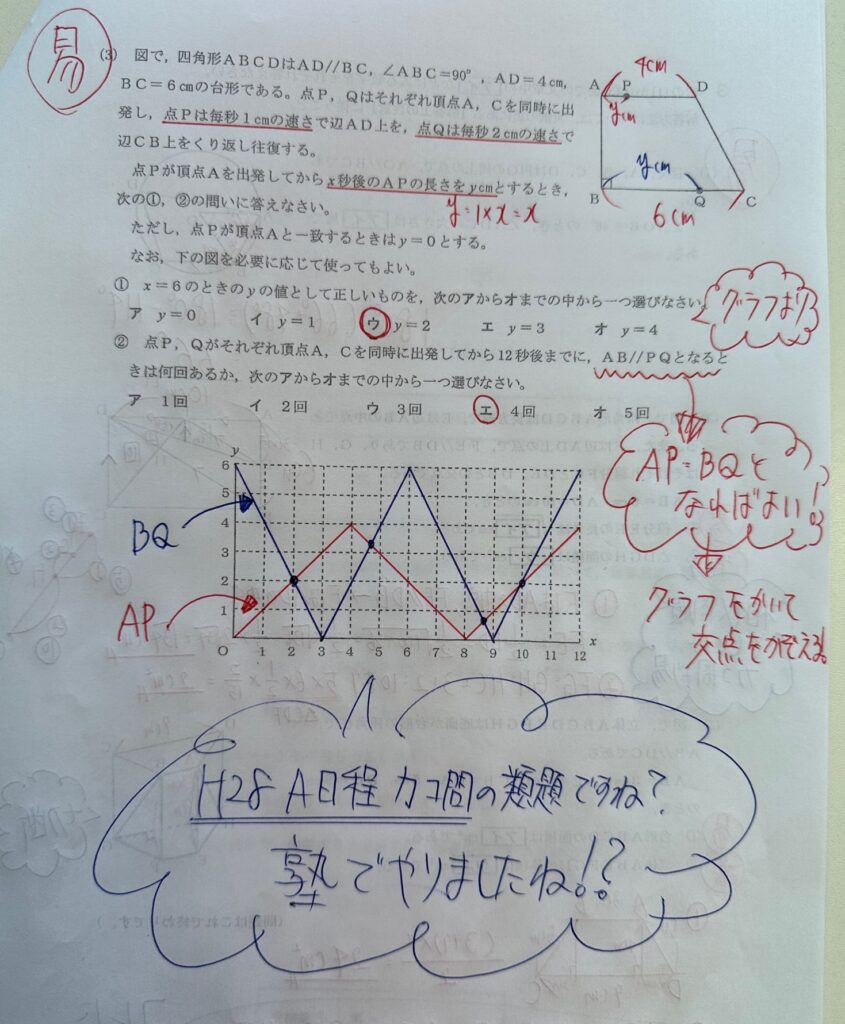
(3)は過去問の類題です。過去問の方がグラフがかきにくかったので難易度上でした。①はグラフをかいて座標を見るだけです。②は過去問同様、グラフをかいて交点を数えるだけです。
大問2は満点必須ですよ!?

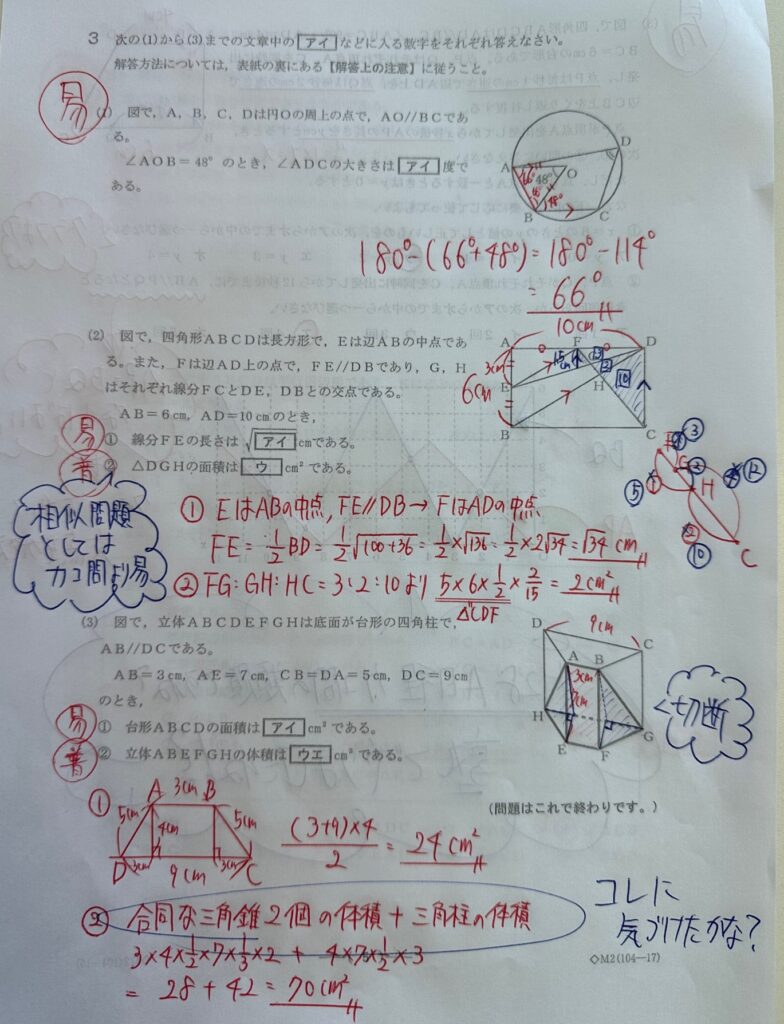
大問3です。
(1)はよくある問題です。底角が等しい、平行線の錯角が等しい、内接する四角形の対角の和は180°を使うだけです。簡単です。
(2)①中点連結定理、つまりFがADの中点であることにきちんと気づけば三平方の定理を使用するだけです。よく見ると…解説で面倒な計算をしていますね(苦笑)…△AEFで三平方の定理を使用すればいきなり出ます!ルート(中身が9+25)=√34
(2)②は過去問で良く出てきたパターンです。FG:GH:HCの何度もあった3つの比が出せれば終わりのものですよね。解答が整数だと確定していますので、出しやすかったと思います。
(3)①の等脚台形からの三平方の定理は何度もやりました。しかも3:4:5のお決まりの比!これもすぐ出せたはずです。
(3)②は難しくはないのですが、切断をして和を求めれば出るというパターンです。塾生が間違えるのであればこの問題だと推測…私の推測!外れてほしい!